• https://pdos.csail.mit.edu/papers/chord:sigcomm01/chord_sigcomm.pdf
• Builds on ideas from
  Paper
  Consistent hashing and random trees
• Published 2003
• Questions
  • Why keep doubling the range of each finger entry, instead of using something linear like this?
    • $$\frac{2^m}{m} \cdot i$$
    • Where $2^m$ is the total number of entries on the circle, $2^m/m$ is the total number of entries a single entry of the $m$-sized routing table can fairly be responsible for
    • The paper answers this a bit later, but the reason is that the number of hops required to find an arbitrary node in a system with $N$ nodes is $O(log N)$, because the number of entries each finger entry is responsible for keeps doubling
  • How is the successor list kept up to date? Does stabilization refresh it along with the finger table?

1. Introduction

• A fundamental problem that confronts peer-to-peer applications is to efficiently locate the node that stores a particular data item. Chord provides support for just one operation: given a key, it maps the key onto a node.

• Communication cost + storage scales logarithmically with cluster size

• The original paper required that nodes were aware of a large fraction of other nodes in the system.

  • Chord nodes only require “routing” info for a few other nodes.
  • In an $N$-node system, each node only needs to maintain information about $O(log N)$ other nodes.
  • Performance degrades gracefully if this information is out of date, assuming at least one piece of information is correct and up to date.

• The entire routing table is maintained across the cluster in aggregate. Nodes joining and leaving update this table, with high probability of doing so using no more than $O(log^2N)$ messages.

2. Related Work

• DNS maps hostnames to IP addresses, and requires a special set of root servers. Chord could do the same sort of mapping without requiring any special servers.
• Other similar systems that map identifiers to some approximation of location: Freenet, Ohaha, Globe, CAN, Pastry, Grid

3: System Model

• Concerns that Chord addresses:
  • Load balancing: keys are spread evenly across nodes
  • Decentralization: no node is more important than any other, no SPOF
  • Scalability: costs grow as the logarithm of the number of nodes
  • Availability: node joins/fails are automatically accounted for
  • Flexible: no assumptions against the structure of keys being looked up
• Chord is intended to be structured as a library liked with applications that use it, exposing two interfaces
  • A lookup(key) function that produces the IP address of a node mapped to key
  • A way to notify the application of changes to the set of keys that a given node is responsible for (as nodes join and data is moved around/etc.)

4: The Base Chord Protocol

• Based on consistent hashing, which, with high probability:
  • Evenly distributes the keyspace across all available nodes
  • Only moves $O(1/N)$ of the keyspace when the $N$th node joins the cluster

Basic algorithm

• Every key is assigned an identifier generated with a base hash function like SHA-1
• Every node is assigned an identifier generated with the same base hash function against the node’s IP
• Identifiers have a fixed length $m$, and are ordered in an identifier circle modulo $2^m$
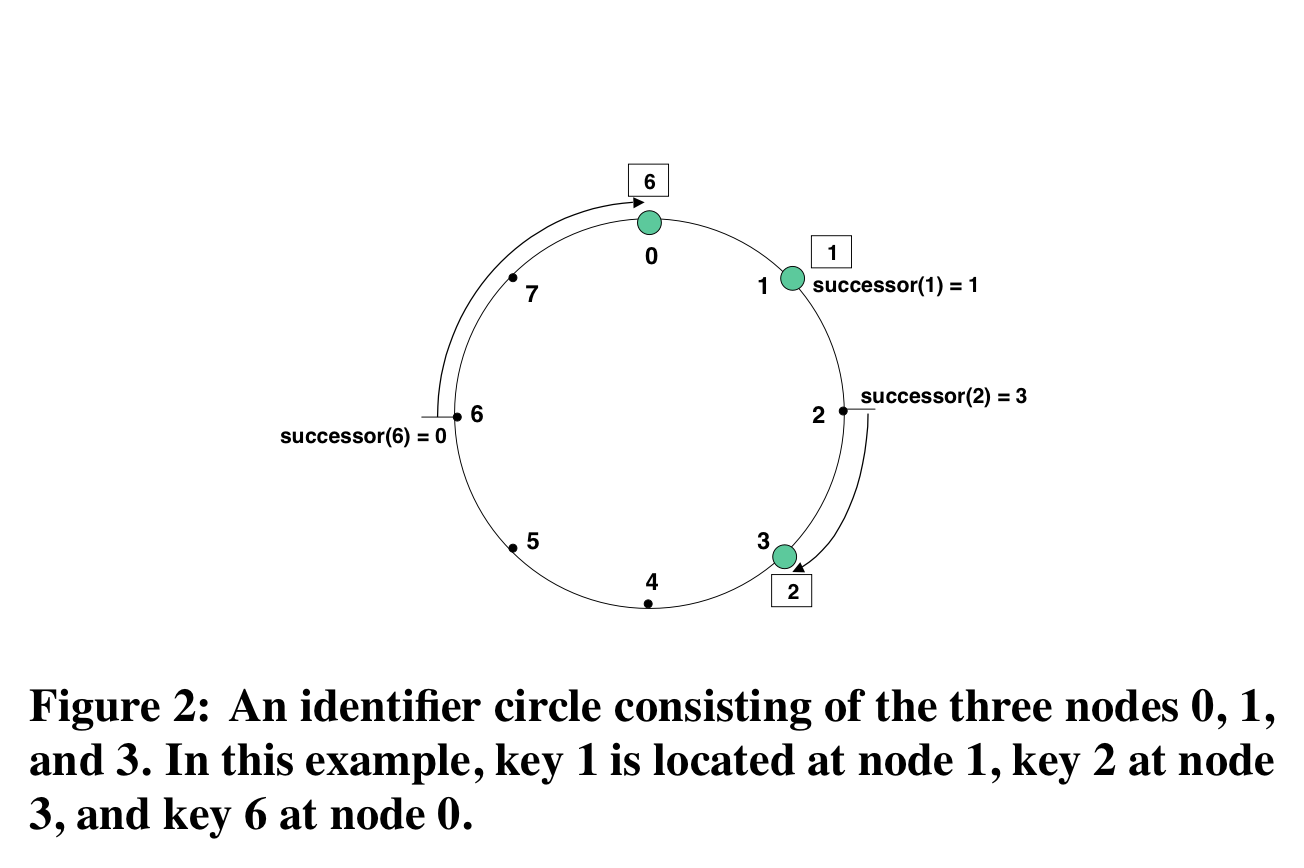
• Key $k$ is assigned to the first node in the circle whose identifier is equal to or follows $k$’s identifier in the circle
• Example
  • 
  • Green circles are nodes, boxed numbers are keys
  • Here keys that hash to:
    • 1: map to node 1
    • 2,3: map to node 3
    • 4,5,6,7,0: map to node 0
• When a node joins the cluster, some of its successor’s keys are reassigned to it
• When a node leaves the cluster, all its keys are reassigned to its successor
• Chord uses a deterministic base hash function like SHA-1 (as opposed to a random function), so the “high probability” claims from the original paper don’t make much sense in the context of an attacker trying to create hash collisions on purpose.
  • Instead, the original axioms (even distribution, small number of movements) hold “based on standard hardness assumptions” (you’d have to break SHA-1 to engineer collisions)
  • This doesn’t say anything about how uniform SHA-1 itself is, though. What if we only use keys that all hash to the a small clustered region of the circle? Virtual nodes?

Virtual nodes

• A physical server is hashed multiple times onto the circle, each with a different identifier. This (presumably) makes it more likely that the gaps between nodes are sized roughly equally.
• The original paper recommends running $O(log N)$ virtual nodes per concrete node
• It’s hard to tell how many nodes a system will end up needing, but a reasonable upper bound is “all IPv4 addresses”
• So in that case, every node runs $log_2(2^{32}) = 32$ virtual nodes

Lookups

• Technically the only piece of information a node needs to perform a lookup is the next node (or successor) in the circle
  • With that in place, a lookup can start at any node and walk the circle until it finds the matching node
  • This is inefficient, though … you have to visit every node in the worst case
  • Chord maintains additional routing information to avoid this, but this is strictly an optimization
• Each node stores a routing table with $m$ entries ($m$ is the number of bits in an identifier)
  • The $i^{th}$ entry in the table contains information about the first server that lies more than $2^{i-1}$ entries past the current node (assuming 1-based indexing, which the paper seems to do)
  • The table is called a finger table, and each server in the routing table is called the $i^{th}$ finger of the node. The first finger is the node’s immediate successor
  • Finger table entries contain the target node’s identifier and its IP address
  • 
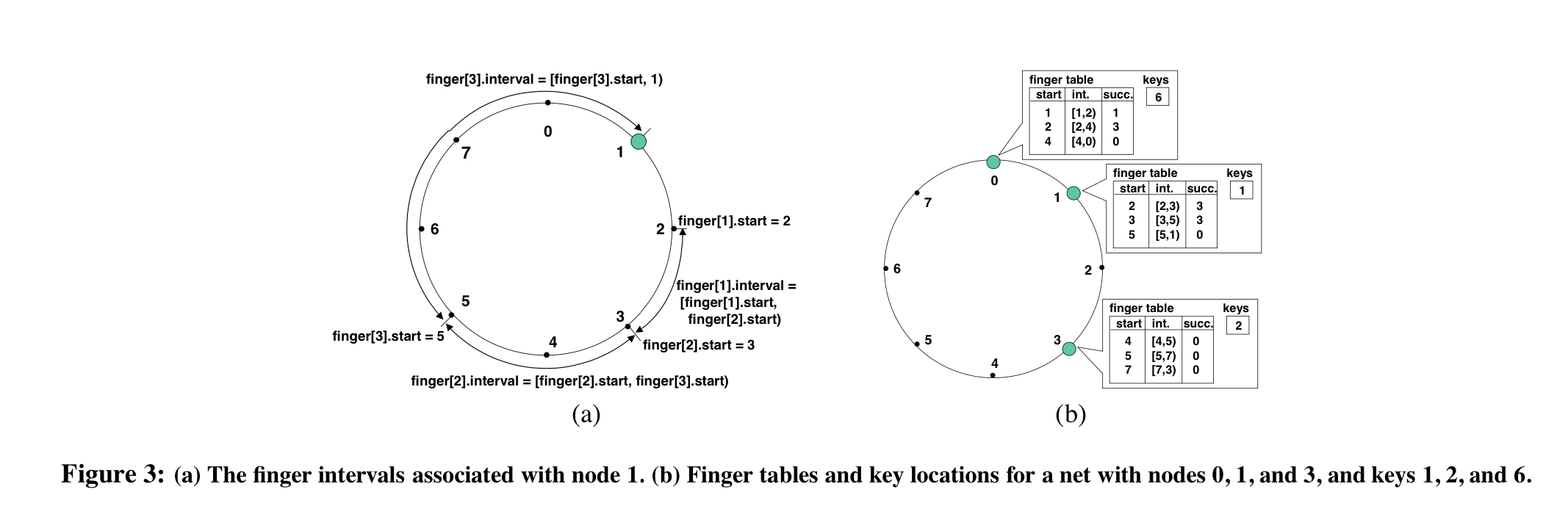
  • Two important characteristics
    1. Each node stores information about only a small number of other nodes, and knows more about nodes closely following it on the identifier circle than about nodes farther away.
    2. A node’s finger table gener- ally does not contain enough information to determine the succes- sor of an arbitrary key.
  • This is because the number of entries that each entry of the routing table is responsible for grows exponentially, with the last one being responsible for $2^{m-1}$ entries (or half the circle).
• When a node doesn’t specifically know the successor for an arbitrary key $k$, it finds the furthest node that precedes $k$’s identifier that it does know about and asks it instead.
  • This may recurse until a node is found such that the $k$’s identifier lies between that node and its successor.
  • 
  • With high probability, the number of nodes that must be contacted to find a successor in an $N$-node network is $O(log N)$.

Adding New Nodes

• Two invariants:
  • Each node’s successor is correctly maintained
  • For every key $k$, its successor is responsible for it
• In addition to the finger table, each node remembers its predecessor in the circle
• With high probability, any node joining or leaving the cluster uses $O(log^2N)$ messages to restore these invariants
  • Here’s how $log^2(x)$ grows (red line) vs. $x$ (blue line) and $log(x)$ (green line)
  • 
• Three things have to happen when a node joins:
  1. Initialize the new node’s predecessor and finger table
  2. Update the finger tables & predecessors for all existing nodes
  3. Notify the application level so it can move keys that have been re-hashed to the new node
• 
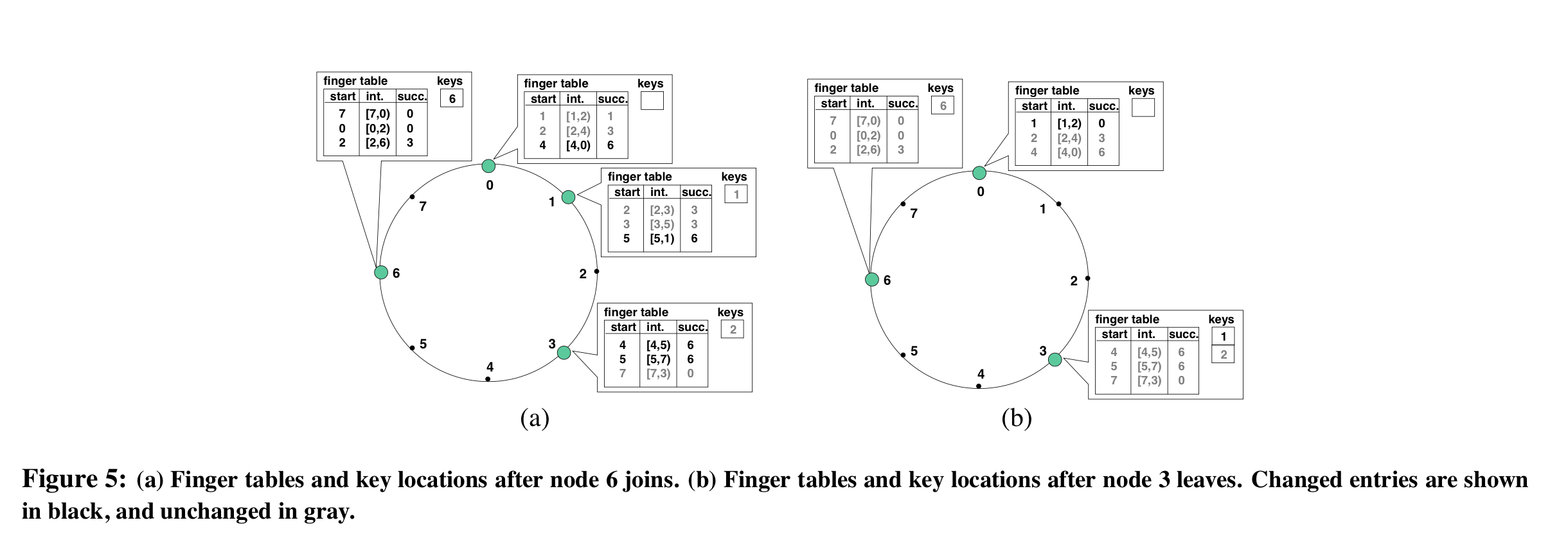
• The new node $n$ contacts a node already in the cluster (say $n'$) and uses it to join the cluster by:
  • Initializing its predecessor and finger tables using $n'$ to perform lookups (finding the successor node for an identifier is Chord’s basic operation)
  • Updating the finger tables of nodes that may put $n$ in their finger tables (for finger $i$, start at $n - 2^{i-1}$ and go backwards, updating all nodes until you hit one with a $finger[i].start$ that precedes $n$)
  • Notifying the application layer so keys can be transferred from $n$’s successor

5. Concurrent Operations and Failures

• Updates to the finger tables when a node joins (ch. 4) won’t always work when multiple nodes join concurrently. Three cases after a few nodes have joined:
  1. All finger tables are still reasonably current, and lookups still happen in $O(log N)$ steps.
  2. Successor pointers are all correct, but fingers are inaccurate. Lookups are still correct but are slower.
  3. Successor pointers are incorrect (or keys haven’t been migrated at the application level). Lookups fail.

Stabilization

• To avoid the third case, use a stabilization scheme that periodically runs to keep successor pointers up to date. This ensures that we’re in case 1/2 most of the time.

• Stabilization by itself won’t correct a Chord system that has split into multiple disjoint cycles, or a single cycle that loops multiple times around the identifier space. These pathological cases cannot be produced by any sequence of ordinary node joins. It is unclear whether they can be produced by network partitions and recoveries or intermittent failures. If produced, these cases could be detected and repaired by periodic sampling of the ring topology.

• Stabilization algorithm

  • A node $n$ runs this process periodically.
  • It asks its successor $n'$ for $n'$’s predecessor. If the predecessor isn’t $n$ itself, correct the inconsistency (either on $n$ or $n'$) and repeat.
  • In addition, refresh/update a random local finger table entry by performing a lookup

• In practice, it sounds like adding a new node could cause a momentary spike in lookup latency.

Failures

• When a node $n$ fails, all finger tables that include that node need to now use the failed node’s successor
• Stabilization should catch this ($n$’s predecessor calls stabilize, and $n$ is unreachable), but what happens next?
• Each node maintains a list of the first $r$ nodes that succeed it. When the successor fails, the node uses the next entry in the list of successors as its successor instead.
• Stabilization across the cluster will eventually correct all finger table entries that contain the failed node.

Replication

The successor-list mechanism also helps higher layer software replicate data. A typical application using Chord might store repli- cas of the data associated with a key at the nodes succeeding the key. The fact that a Chord node keeps track of its successors means that it can inform the higher layer software when successors come and go, and thus when the software should propagate new replicas.